16 因子

16.1 引言

因子 (factor) 用于处理分类变量，即那些具有固定且已知的一组可能值的变量。当你希望以非字母顺序显示字符向量时，因子也很有用。

我们将首先阐述为什么数据分析需要因子¹，以及你如何用 factor() 创建它们。接着，我们将向你介绍 gss_cat 数据集，其中包含大量分类变量供你试验。然后，你将使用该数据集练习修改因子的顺序和值，最后我们以讨论有序因子作为结束。

16.1.1 先决条件

R base 提供了一些创建和操作因子的基本工具。我们将用 forcats 包来补充这些工具，该包是核心 tidyverse 的一部分。它提供了一系列处理分类变量 (categorical variables) 的工具（并且它也是 factors 的一个字母重组词！），包含了大量用于处理因子的辅助函数。

library(tidyverse)

16.2 因子基础

假设你有一个记录月份的变量：

x1 <- c("Dec", "Apr", "Jan", "Mar")

使用字符串来记录这个变量有两个问题：

只有十二个可能的月份，但没有任何东西能防止你打字错误：
```
x2 <- c("Dec", "Apr", "Jam", "Mar")
```
它的排序方式没有用处：
```
sort(x1)
#> [1] "Apr" "Dec" "Jan" "Mar"
```

你可以用因子来解决这两个问题。要创建一个因子，你必须首先创建一个有效水平 (levels) 的列表：

month_levels <- c(
  "Jan", "Feb", "Mar", "Apr", "May", "Jun", 
  "Jul", "Aug", "Sep", "Oct", "Nov", "Dec"
)

现在你可以创建一个因子：

y1 <- factor(x1, levels = month_levels)
y1
#> [1] Dec Apr Jan Mar
#> Levels: Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec

sort(y1)
#> [1] Jan Mar Apr Dec
#> Levels: Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec

任何不在水平中的值都会被静默地转换为 NA：

y2 <- factor(x2, levels = month_levels)
y2
#> [1] Dec  Apr  <NA> Mar 
#> Levels: Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec

这看起来有风险，所以你可能想改用 forcats::fct()：

y2 <- fct(x2, levels = month_levels)
#> Error in `fct()`:
#> ! All values of `x` must appear in `levels` or `na`
#> ℹ Missing level: "Jam"

如果你省略了水平，它们将从数据中按字母顺序提取：

factor(x1)
#> [1] Dec Apr Jan Mar
#> Levels: Apr Dec Jan Mar

按字母顺序排序有点风险，因为并非每台计算机都会以相同的方式对字符串进行排序。所以 forcats::fct() 会按首次出现的顺序排序：

fct(x1)
#> [1] Dec Apr Jan Mar
#> Levels: Dec Apr Jan Mar

如果你需要直接访问有效的水平集，你可以使用 levels()：

levels(y2)
#>  [1] "Jan" "Feb" "Mar" "Apr" "May" "Jun" "Jul" "Aug" "Sep" "Oct" "Nov" "Dec"

你也可以在使用 readr 读取数据时，通过 col_factor() 创建一个因子：

csv <- "
month,value
Jan,12
Feb,56
Mar,12"

df <- read_csv(csv, col_types = cols(month = col_factor(month_levels)))
df$month
#> [1] Jan Feb Mar
#> Levels: Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec

16.3 综合社会调查

在本章的其余部分，我们将使用 forcats::gss_cat。这是来自综合社会调查 (General Social Survey) 的数据样本，该调查是由芝加哥大学的独立研究机构 NORC 进行的一项长期美国调查。该调查有数千个问题，在 gss_cat 中，Hadley 选择了一小部分，用以说明你在处理因子时会遇到的一些常见挑战。

gss_cat
#> # A tibble: 21,483 × 9
#>    year marital         age race  rincome        partyid           
#>   <int> <fct>         <int> <fct> <fct>          <fct>             
#> 1  2000 Never married    26 White $8000 to 9999  Ind,near rep      
#> 2  2000 Divorced         48 White $8000 to 9999  Not str republican
#> 3  2000 Widowed          67 White Not applicable Independent       
#> 4  2000 Never married    39 White Not applicable Ind,near rep      
#> 5  2000 Divorced         25 White Not applicable Not str democrat  
#> 6  2000 Married          25 White $20000 - 24999 Strong democrat   
#> # ℹ 21,477 more rows
#> # ℹ 3 more variables: relig <fct>, denom <fct>, tvhours <int>

（请记住，由于这个数据集是由一个包提供的，你可以使用 ?gss_cat 获取更多关于变量的信息。）

当因子存储在 tibble 中时，你无法轻易看到它们的水平。一种查看它们的方法是使用 count()：

gss_cat |>
  count(race)
#> # A tibble: 3 × 2
#>   race      n
#>   <fct> <int>
#> 1 Other  1959
#> 2 Black  3129
#> 3 White 16395

在处理因子时，两个最常见的操作是改变水平的顺序和改变水平的值。这些操作将在下面的章节中描述。

16.3.1 练习

探索 rincome（报告的收入）的分布。是什么使得默认的条形图难以理解？你如何改进这个图？
在这次调查中，最常见的 relig（宗教）是什么？最常见的 partyid（政党认同）是什么？
denom（教派）适用于哪个 relig？你如何通过表格找出答案？你如何通过可视化找出答案？

16.4 修改因子顺序

在可视化中改变因子水平的顺序通常很有用。例如，假设你想探索不同宗教每天平均观看电视的小时数：

relig_summary <- gss_cat |>
  group_by(relig) |>
  summarize(
    tvhours = mean(tvhours, na.rm = TRUE),
    n = n()
  )

ggplot(relig_summary, aes(x = tvhours, y = relig)) +
  geom_point()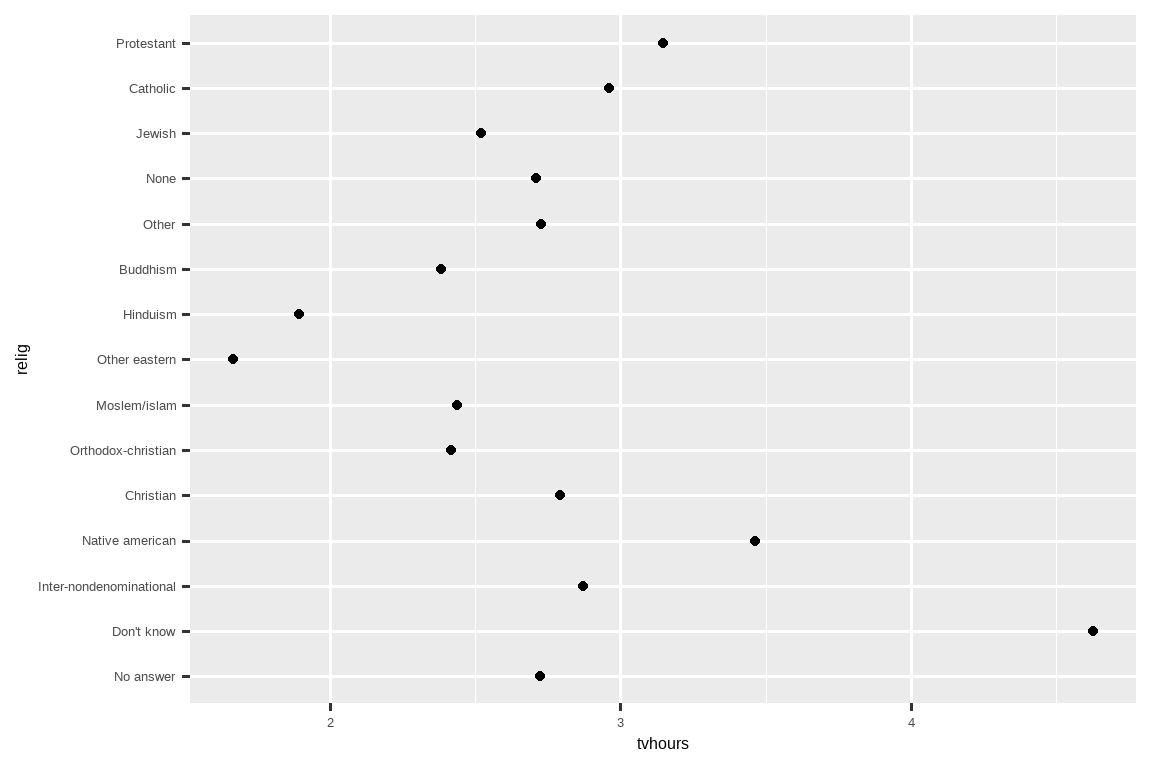

一个散点图，x 轴为 tvhours，y 轴为 religion。 y 轴的排序看起来是任意的，这使得很难看出整体模式。

这个图很难读，因为没有整体模式。我们可以通过使用 fct_reorder() 来重新排序 relig 的水平来改进它。fct_reorder() 接受三个参数：

.f，你想要修改其水平的因子。
.x，你想要用来重新排序水平的数值向量。
可选的 .fun，一个函数，如果 .f 的每个值对应多个 .x 的值，则使用该函数。默认值是 median。

ggplot(relig_summary, aes(x = tvhours, y = fct_reorder(relig, tvhours))) +
  geom_point()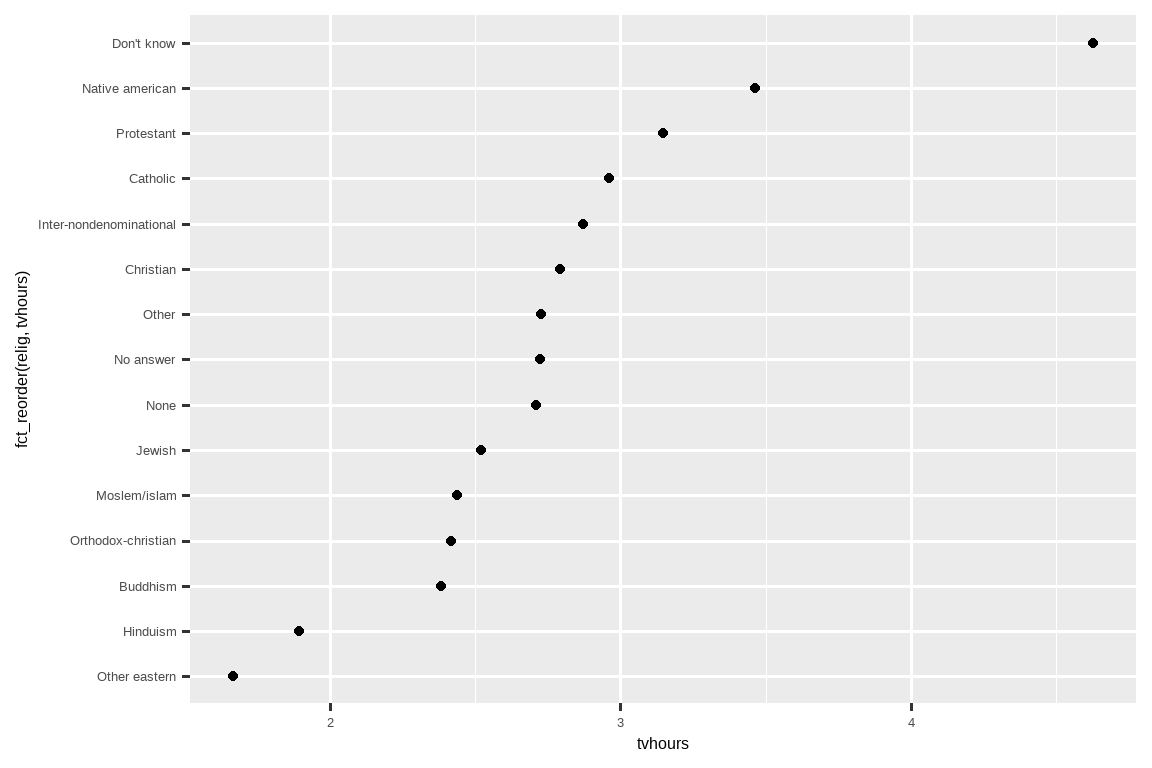

与上图相同的散点图，但现在 religion 按 tvhours 的升序显示。 "Other eastern" 的 tvhours 最少，不到 2 小时，而 "Don't know" 最高（超过 5 小时）。

重新排序宗教使得更容易看出“不知道”类别的人看电视的时间要多得多，而印度教和其他东方宗教的人看电视的时间要少得多。

当你开始进行更复杂的转换时，我们建议将它们从 aes() 中移出，放到一个单独的 mutate() 步骤中。例如，你可以像下面这样重写上面的图：

relig_summary |>
  mutate(
    relig = fct_reorder(relig, tvhours)
  ) |>
  ggplot(aes(x = tvhours, y = relig)) +
  geom_point()

如果我们创建一个类似的图，看看平均年龄在不同报告收入水平上是如何变化的呢？

rincome_summary <- gss_cat |>
  group_by(rincome) |>
  summarize(
    age = mean(age, na.rm = TRUE),
    n = n()
  )

ggplot(rincome_summary, aes(x = age, y = fct_reorder(rincome, age))) +
  geom_point()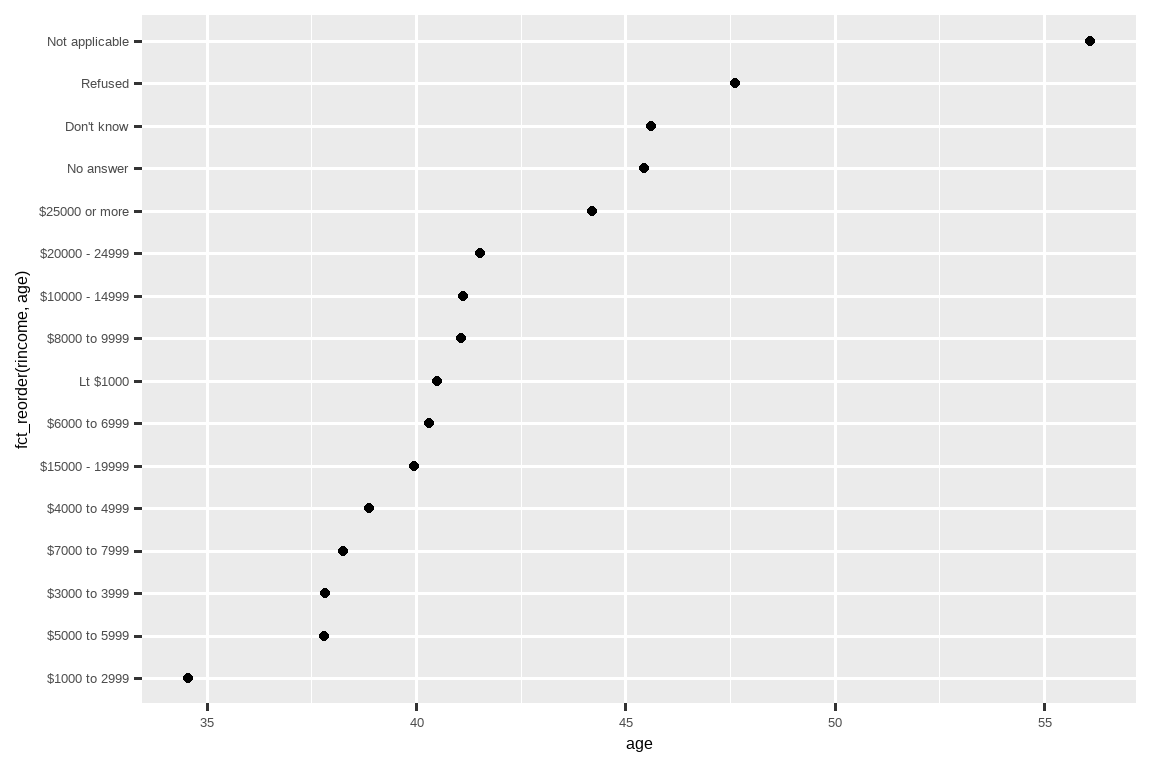

一个散点图，x 轴为 age，y 轴为 income。income 已按平均年龄重新排序，但这没什么意义。y 轴的一个部分从 $6000-6999，然后是 <$1000，再然后是 $8000-9999。

在这里，任意重新排序水平不是一个好主意！这是因为 rincome 已经有了一个我们不应该打乱的原则性顺序。请将 fct_reorder() 保留给那些水平是任意排序的因子。

然而，将“不适用 (Not applicable)”和其他特殊水平一起移到前面是有意义的。你可以使用 fct_relevel()。它接受一个因子 .f，然后是任意数量的你想要移到最前面的水平。

ggplot(rincome_summary, aes(x = age, y = fct_relevel(rincome, "Not applicable"))) +
  geom_point()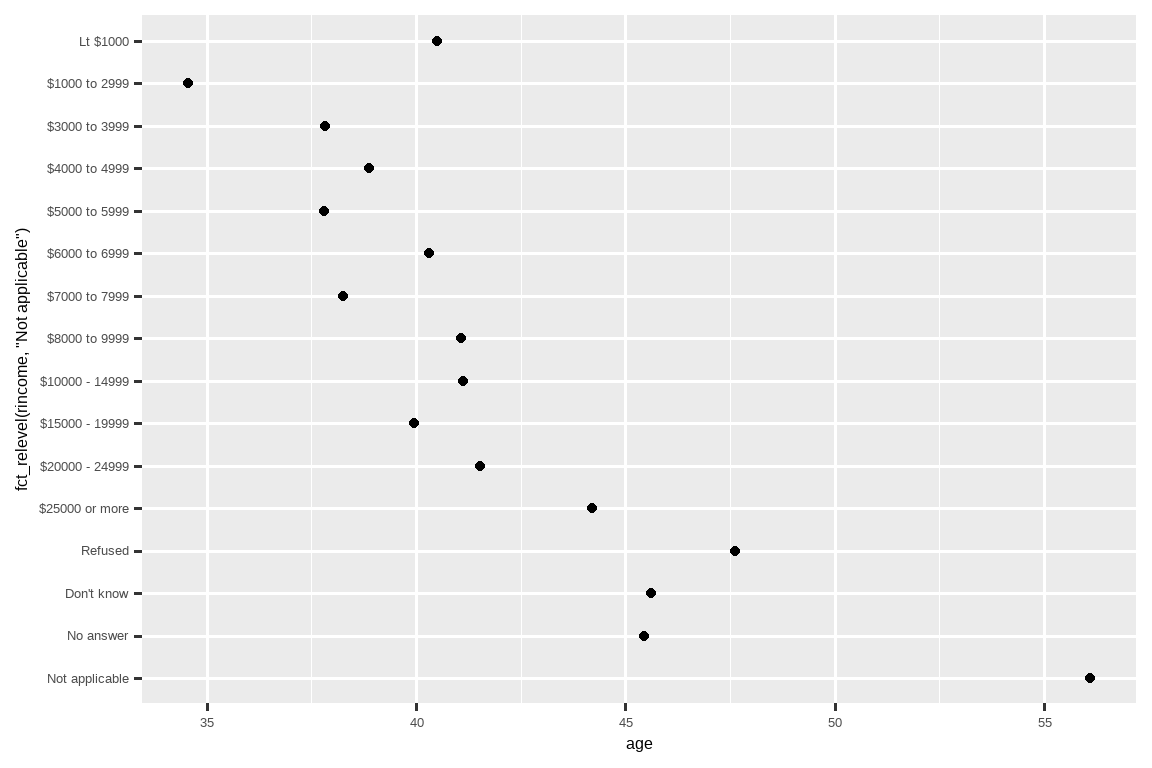

与上图相同的散点图，但现在 "Not Applicable" 显示在 y 轴的底部。总的来说，收入和年龄之间存在正相关关系，而平均年龄最高的收入区间是 "Not applicable"。

你认为为什么“不适用”的平均年龄这么高？

当你在图上为线条着色时，另一种类型的重新排序也很有用。fct_reorder2(.f, .x, .y) 通过与最大 .x 值相关联的 .y 值来重新排序因子 .f。这使得图更容易阅读，因为图右侧的线条颜色将与图例对齐。

by_age <- gss_cat |>
  filter(!is.na(age)) |>
  count(age, marital) |>
  group_by(age) |>
  mutate(
    prop = n / sum(n)
  )

ggplot(by_age, aes(x = age, y = prop, color = marital)) +
  geom_line(linewidth = 1) +
  scale_color_brewer(palette = "Set1")

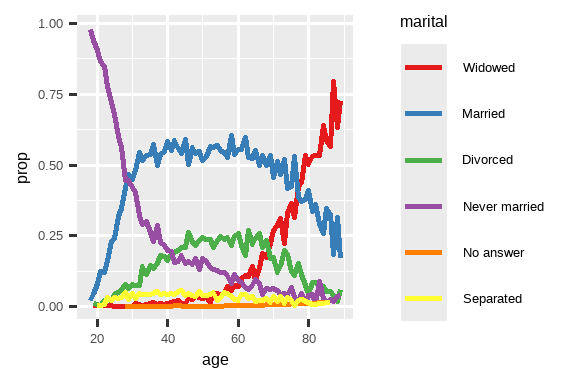
ggplot(by_age, aes(x = age, y = prop, color = fct_reorder2(marital, age, prop))) +
  geom_line(linewidth = 1) +
  scale_color_brewer(palette = "Set1") +
  labs(color = "marital")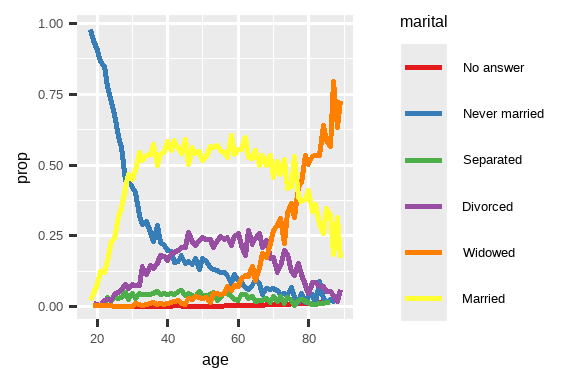

一个线图，x 轴为 age，y 轴为 proportion。每种婚姻状况都有一条线：无答案、从未结婚、分居、离婚、丧偶和已婚。这个图有点难读，因为图例的顺序与图上的线条无关。重新排列图例使得图更容易阅读，因为图例颜色现在与图右侧线条的顺序相匹配。你可以看到一些不出所料的模式：从未结婚的比例随年龄增长而下降，已婚的比例呈倒 U 形，丧偶的比例开始时很低，但在 60 岁后急剧增加。

最后，对于条形图，你可以使用 fct_infreq() 按频率降序排列水平：这是最简单的重新排序类型，因为它不需要任何额外的变量。如果你希望它们按频率升序排列，可以与 fct_rev() 结合使用，这样在条形图中最大的值就会在右边，而不是左边。

gss_cat |>
  mutate(marital = marital |> fct_infreq() |> fct_rev()) |>
  ggplot(aes(x = marital)) +
  geom_bar()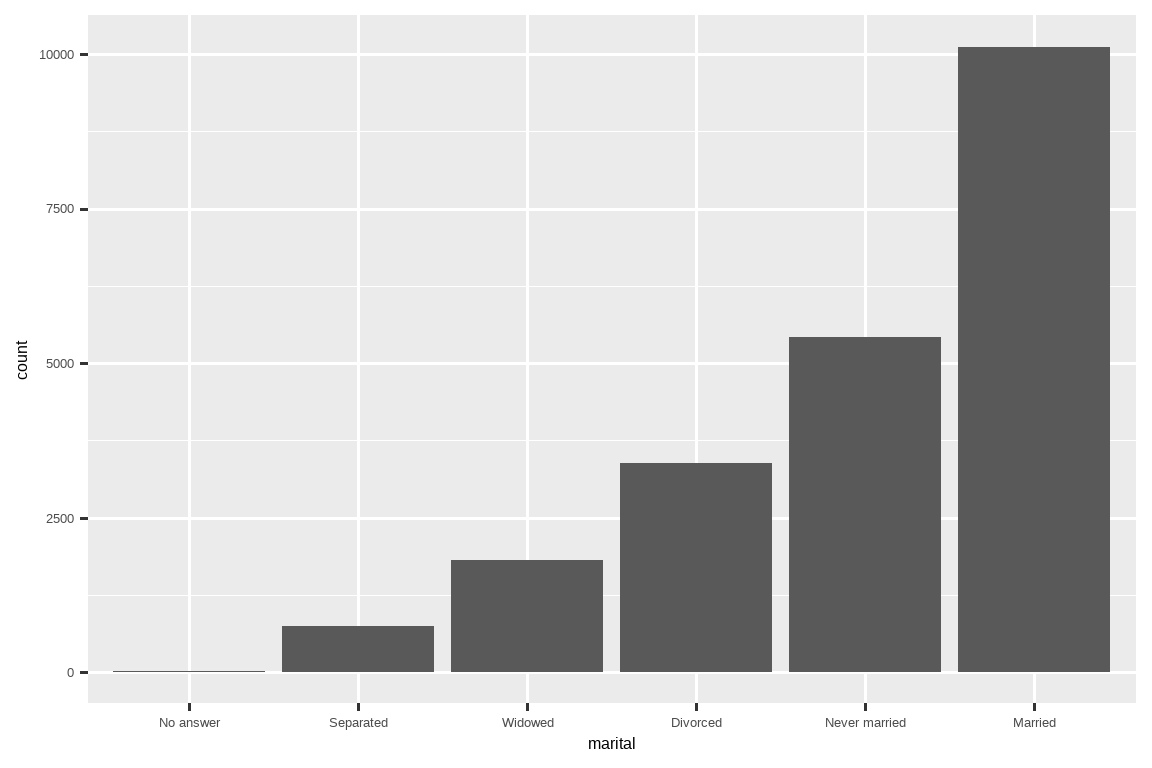

一个婚姻状况的条形图，从最少到最常见排序：无答案（~0）、分居（~1,000）、丧偶（~2,000）、离婚（~3,000）、从未结婚（~5,000）、已婚（~10,000）。

16.4.1 练习

tvhours 中有一些可疑的高数值。均值是一个好的汇总统计量吗？
对于 gss_cat 中的每个因子，判断其水平的顺序是任意的还是有原则的。
为什么将“不适用 (Not applicable)”移到水平的前面会使它移动到图的底部？

16.5 修改因子水平

比改变水平顺序更强大的是改变它们的值。这可以让你为出版物澄清标签，并为高层次的展示折叠水平。最通用和最强大的工具是 fct_recode()。它允许你重编码或更改每个水平的值。例如，以 gss_cat 数据框中的 partyid 变量为例：

gss_cat |> count(partyid)
#> # A tibble: 10 × 2
#>   partyid                n
#>   <fct>              <int>
#> 1 No answer            154
#> 2 Don't know             1
#> 3 Other party          393
#> 4 Strong republican   2314
#> 5 Not str republican  3032
#> 6 Ind,near rep        1791
#> # ℹ 4 more rows

这些水平很简短且不一致。让我们调整它们，让它们更长并使用平行的结构。像 tidyverse 中大多数重命名和重编码函数一样，新值在左边，旧值在右边：

gss_cat |>
  mutate(
    partyid = fct_recode(partyid,
      "Republican, strong"    = "Strong republican",
      "Republican, weak"      = "Not str republican",
      "Independent, near rep" = "Ind,near rep",
      "Independent, near dem" = "Ind,near dem",
      "Democrat, weak"        = "Not str democrat",
      "Democrat, strong"      = "Strong democrat"
    )
  ) |>
  count(partyid)
#> # A tibble: 10 × 2
#>   partyid                   n
#>   <fct>                 <int>
#> 1 No answer               154
#> 2 Don't know                1
#> 3 Other party             393
#> 4 Republican, strong     2314
#> 5 Republican, weak       3032
#> 6 Independent, near rep  1791
#> # ℹ 4 more rows

fct_recode() 会保持未明确提及的水平不变，并且如果你意外地引用了不存在的水平，它会警告你。

要组合组别，你可以将多个旧水平分配给同一个新水平：

gss_cat |>
  mutate(
    partyid = fct_recode(partyid,
      "Republican, strong"    = "Strong republican",
      "Republican, weak"      = "Not str republican",
      "Independent, near rep" = "Ind,near rep",
      "Independent, near dem" = "Ind,near dem",
      "Democrat, weak"        = "Not str democrat",
      "Democrat, strong"      = "Strong democrat",
      "Other"                 = "No answer",
      "Other"                 = "Don't know",
      "Other"                 = "Other party"
    )
  )

请谨慎使用这种技术：如果你将真正不同的类别组合在一起，你最终会得到误导性的结果。

如果你想折叠很多水平，fct_collapse() 是 fct_recode() 的一个有用变体。对于每个新变量，你可以提供一个旧水平的向量：

gss_cat |>
  mutate(
    partyid = fct_collapse(partyid,
      "other" = c("No answer", "Don't know", "Other party"),
      "rep" = c("Strong republican", "Not str republican"),
      "ind" = c("Ind,near rep", "Independent", "Ind,near dem"),
      "dem" = c("Not str democrat", "Strong democrat")
    )
  ) |>
  count(partyid)
#> # A tibble: 4 × 2
#>   partyid     n
#>   <fct>   <int>
#> 1 other     548
#> 2 rep      5346
#> 3 ind      8409
#> 4 dem      7180

有时你只是想把小的组别集中在一起，以简化图表或表格。这就是 fct_lump_*() 系列函数的工作。fct_lump_lowfreq() 是一个简单的起点，它逐步将最小的组别类别归入“Other”，并始终保持“Other”为最小的类别。

gss_cat |>
  mutate(relig = fct_lump_lowfreq(relig)) |>
  count(relig)
#> # A tibble: 2 × 2
#>   relig          n
#>   <fct>      <int>
#> 1 Protestant 10846
#> 2 Other      10637

在这种情况下，它不是很有帮助：这次调查中大多数美国人确实是新教徒，但我们可能想看到更多细节！相反，我们可以使用 fct_lump_n() 来指定我们想要恰好 10 个组别：

gss_cat |>
  mutate(relig = fct_lump_n(relig, n = 10)) |>
  count(relig, sort = TRUE)
#> # A tibble: 10 × 2
#>   relig          n
#>   <fct>      <int>
#> 1 Protestant 10846
#> 2 Catholic    5124
#> 3 None        3523
#> 4 Christian    689
#> 5 Other        458
#> 6 Jewish       388
#> # ℹ 4 more rows

阅读文档以了解 fct_lump_min() 和 fct_lump_prop()，它们在其他情况下很有用。

16.5.1 练习

认同为民主党、共和党和独立派的人的比例随时间有何变化？
你如何将 rincome 折叠成一小组类别？
注意在上面的 fct_lump 示例中有 9 个组（不包括 other）。为什么不是 10 个？（提示：输入 ?fct_lump，找到 other_level 参数的默认值是 “Other”。）

16.6 有序因子

在继续之前，有必要简要提及一种特殊类型的因子：有序因子 (ordered factors)。用 ordered() 函数创建的有序因子意味着水平之间存在严格的顺序，但没有指定水平之间差异的大小。当你知道水平有排名，但没有精确的数值排名时，你会使用有序因子。

当一个有序因子被打印时，你可以识别它，因为它在因子水平之间使用 < 符号：

ordered(c("a", "b", "c"))
#> [1] a b c
#> Levels: a < b < c

在 R base 和 tidyverse 中，有序因子的行为与常规因子非常相似。只有在两个地方你可能会注意到不同的行为：

如果你在 ggplot2 中将一个有序因子映射到颜色或填充，它将默认为 scale_color_viridis()/scale_fill_viridis()，这是一个暗示排名的颜色标度。
如果你在线性模型中使用一个有序预测变量，它将使用“多项式对比”。这些有点用，但除非你有统计学博士学位，否则你不太可能听说过它们，即使那样，你可能也不常解释它们。如果你想了解更多，我们推荐 Lisa DeBruine 的 vignette("contrasts", package = "faux")。

就本书而言，正确区分常规因子和有序因子并不是特别重要。然而，在更广泛的范围内，某些领域（特别是社会科学）确实广泛使用有序因子。在这些背景下，正确识别它们很重要，以便其他分析包可以提供适当的行为。

16.7 总结

本章向你介绍了用于处理因子的便捷 forcats 包，并介绍了最常用的函数。forcats 包含了我们没有篇幅在这里讨论的各种其他辅助函数，所以每当你遇到以前没有遇到过的因子分析挑战时，我强烈建议你浏览一下参考索引，看看是否有现成的函数可以帮助解决你的问题。

如果你在阅读本章后想了解更多关于因子的信息，我们推荐阅读 Amelia McNamara 和 Nicholas Horton 的论文 Wrangling categorical data in R。这篇论文阐述了在 stringsAsFactors: An unauthorized biography 和 stringsAsFactors = <sigh> 中讨论的一些历史，并比较了本书中概述的 tidyverse 分类数据处理方法与 R base 方法。该论文的早期版本帮助激发和确定了 forcats 包的范围；感谢 Amelia 和 Nick！

在下一章中，我们将转换方向，开始学习 R 中的日期和时间。日期和时间看起来 deceptively 简单，但你很快就会看到，你对它们了解得越多，它们似乎就变得越复杂！

它们对于建模也非常重要。↩︎